
I’ve already made the case in several blog posts (part 1, part 2, part 3) that using survival analysis can improve churn prediction.
In this blog post I’ll show another use case where survival analysis can improve on common practices: A/B testing!
The problems with common A/B testing practices
Usually when running an A/B test analysts assign users randomly to variants over time and measure conversion rate as the ratio between the number of conversions and the number of users in each variant. Users who just entered the test and those who are in the test for 2 weeks get the same weight.
This can be enough for cases where a conversion either happens or not within a short time frame after assignment to a variant (e.g. Finishing an on-boarding flow).
There are however many instances where conversions are spread over a longer time frame. One example would be first order after visiting a site landing page. Such conversions may happen within minutes, but a large churn could also happen within days after the first visit.
In such cases the business KPIs are usually “bounded” to a certain period - e.g. “conversion within 7 days” or “churn within 1 month”.
In those instance measuring conversions without considering their timing has 2 major flaws:
- It makes the statistic we’re measuring unintelligible - Average conversions at any point in time does not translate to any bounded metric. In fact as the test keeps running - conversion rates will increase just because users get more time to convert. The experiment results will be thus hard to relate to the business KPIs.
- It discards the timing information which could lead to reduced power compared with methods that do take conversion timing into account.
To demonstrate point #2 we’ll run a small simulation study
Simulation study
We’ll have users join the experiment randomly over a 30 day period. Users’ time to convert will be simulated from a Weibull distribution with scale \(\sigma = 30,000\) and \(\alpha_{\text{ctrl}}=0.18\) for the control group and \(\alpha_{\text{trt}}=0.157\) for the treatment group.
Below are the corresponding survival curves:
alpha_ctrl <- 0.18
alpha_trt <- 0.157
sigma <- 30000
conv_7d_ctrl <- format_pct(pweibull(7, alpha_ctrl, sigma))
conv_7d_trt <- format_pct(pweibull(7, alpha_trt, sigma))
t <- seq(0, 7, 0.1)
surv_ctrl <- 1 - pweibull(t, alpha_ctrl, sigma)
surv_trt <- 1 - pweibull(t, alpha_trt, sigma)
plot(t, surv_trt, type = "line", col = "red", ylab = "S(t)", xlab = "t (days)",
ylim = c(0.7, 1))
lines(t, surv_ctrl, col = "black")
legend("topright",
col = c("black", "red"), legend = c("Control", "Treatment"), lty = 1,
title = "Variant"
)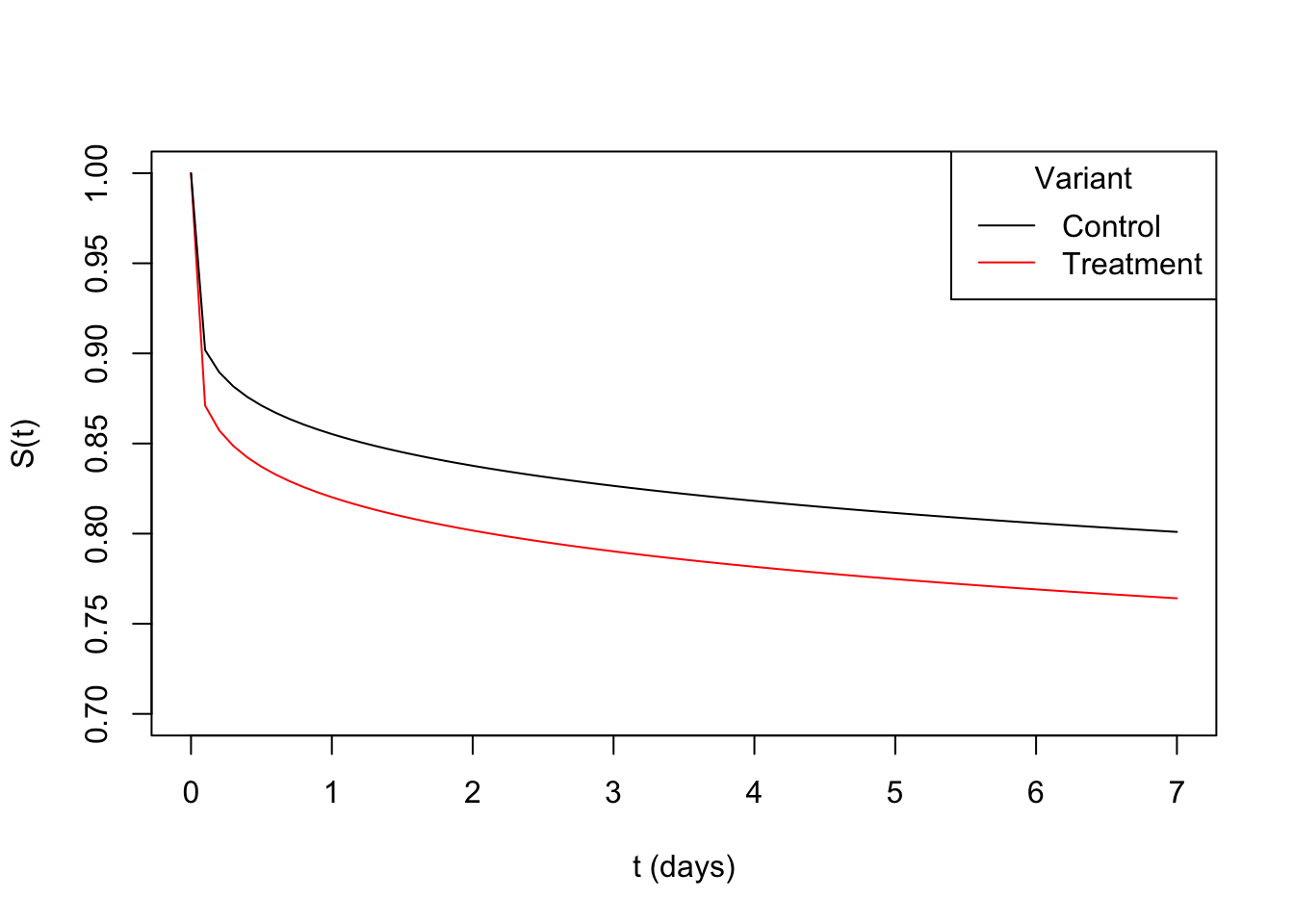
Assuming we’re interested with conversions within 7 days, the true (unknown) conversion rate in the control group is 19.9% and in the treatment is 23.6%.
Below is the function which will generate the simulation data:
n <- 2000
test_duration <- 30
gen_surv_data <- function(m, alpha){
set.seed(m)
tstart <- runif(n, 0, test_duration)
tconvert <- rweibull(n, alpha, sigma)
status <- as.integer(tstart + tconvert < test_duration)
tstatus <- ifelse(status == 0, test_duration - tstart, tconvert)
return(data.frame(tstatus=tstatus, status=status))
}To demonstrate the benefits of using survival in A/B testing we’ll compare the power of test 3 statistics:
- T-test on conversions (the common procedure)
- T-test on 7 day conversion (estimated using a Kaplan-Meier curve)
- Peto & Peto modification of the Gehan-Wilcoxon test
Below is the code that implements the above:
run_simulation <- function(m, alpha1, alpha2){
data_1 <- gen_surv_data(m, alpha1)
data_2 <- gen_surv_data(m+1, alpha2)
# T-test on conversions (the common procedure):
p1_hat <- mean(data_1$status)
p1_var <- p1_hat*(1-p1_hat)/length(data_1$status)
p2_hat <- mean(data_2$status)
p2_var <- p2_hat*(1-p2_hat)/length(data_2$status)
stat <- abs(p2_hat - p1_hat)/sqrt(p1_var + p2_var)
ans1 <- pnorm(stat, lower.tail = F)*2
# T-test on 7 day conversion (estimated using a Kaplan-Meier curve):
data_1$variant <- "control"
data_2$variant <- "treatment"
surv_data <- rbind(data_1, data_2)
surv_model <- summary(survfit(Surv(tstatus, status)~variant, data = surv_data),
times = 7, extend = T)
p1_hat <- 1 - surv_model$surv[1]
p1_var <- surv_model$std.err[1]^2
p2_hat <- 1 - surv_model$surv[2]
p2_var <- surv_model$std.err[2]^2
stat <- abs(p2_hat - p1_hat)/sqrt(p1_var + p2_var)
ans2 <- pnorm(stat, lower.tail = F)*2
# Peto & Peto modification of the Gehan-Wilcoxon test:
mgw_test <- survdiff(Surv(tstatus, status)~variant, data = surv_data, rho = 1)
ans3 <- mgw_test$pvalue
return(data.frame(`T-test conversions` = ans1, `T-test KM 7 day conversion` = ans2,
`Modified Gehan-Wilcoxon test` = ans3, check.names = F))
}Before measuring power let’s verify our statistics satisfy the desired false positive rate \(\alpha = 0.05\) (5%) when both variants have the same conversion rates:
alpha <- 0.05
M <- 500
res <- Reduce("rbind", lapply(1:M, function(m) run_simulation(m, alpha_ctrl, alpha_ctrl)))
res <- data.frame(Statistic = names(res),
`False positive rate` = format_pct(sapply(res, function(x) mean(x<=alpha))),
check.names = F, row.names = NULL)
knitr::kable(res, align = "c")| Statistic | False positive rate |
|---|---|
| T-test conversions | 5.6% |
| T-test KM 7 day conversion | 5.2% |
| Modified Gehan-Wilcoxon test | 5.8% |
Looks good.
Next, let’s examine power:
M <- 2000
res <- Reduce("rbind", lapply(1:M, function(m) run_simulation(m, alpha_ctrl, alpha_trt)))
res <- data.frame(Statistic = names(res),
Power = sapply(res, function(x) mean(x<=alpha)),
check.names = F, row.names = NULL)
uplift_logrank <- format_pct((res[3,2] - res[1,2])/res[1,2])
uplift_km <- format_pct((res[2,2] - res[1,2])/res[1,2])
res$Power <- format_pct(res$Power)
knitr::kable(res, align = "c")| Statistic | Power |
|---|---|
| T-test conversions | 77.7% |
| T-test KM 7 day conversion | 78.3% |
| Modified Gehan-Wilcoxon test | 85% |
While the T-test on KM 7 day conversion relates better to business KPIs than the T-test on conversions (the common procedure), it is only marginally more powerful.
The modified Gehan-Wilcoxon statistic on the other hand yields a substantial uplift in power, while only weakly relating to the business KPIs like the regular conversions T-test.
It should be noted that the power gains vary somewhat according to the point compared on the survival curve, the actual survival curve shape, experiment duration etc.
In a future post I hope to further explore this topic over a wider set of scenarios and test statistics (The ComparisonSurv package in R looks promising).
Summary
When doing A/B testing in scenarios where time to convert varies - it’s often useful to apply survival analysis to take advantage of the time dimension. Either compare a point of interest on the survival curve to make the result relate directly to the business KPIs, or use the modified Gehan-Wilcoxon statistic statistic for improved power.